Phosphor materials are often used in illumination systems for creating white light sources. This article describes modeling a phosphorescent material, as often used to generate white light sources in illumination systems, via the Phosphor.DLL bulk scattering model in OpticStudio.
Authored By Sanjay Gangadhara
Downloads
Introduction
Phosphor materials are often used to create white light sources. Typically, a blue light LED is placed adjacent to a phosphor which converts some fraction of the light to a longer wavelength (e.g. yellow) via fluorescence. Color-mixing of the input and converted beams results in white emission to the human eye.
Fluorescence is modeled in OpticStudio as a bulk scattering event that may take one of many distribution profiles. In a phosphorescent system, the input beam may also scatter and undergo a different distrubtion independent of "fluorescence scattering". The Phosphor DLL provided with OpticStudio has been developed to describe such a system.
Description of the model
To model a volume as a phosphorescent material in Non-Sequential mode, select the Phosphor.DLL file under the Volume Physics tab of the object properties:
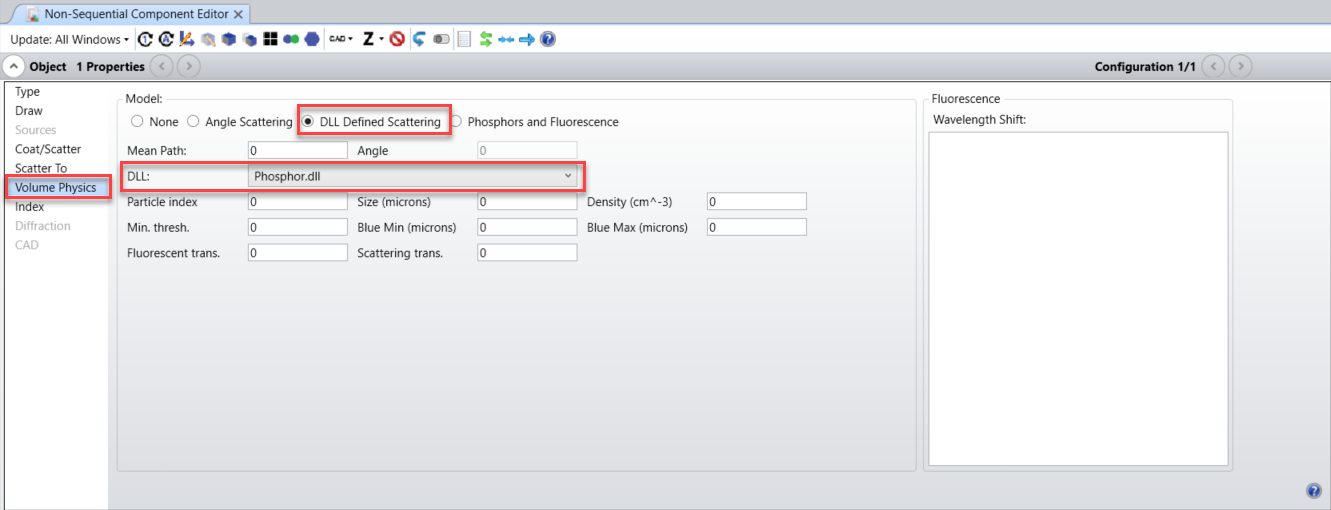
This DLL models a material in which light can undergo fluorescence and “real” bulk scattering. The fluorescence distribution is given by the “Angle Scattering” model, i.e. light which fluoresces will be scattered with uniform probability into a sphere (the half cone angle is 180 degrees with respect to the input ray). The bulk scattering distribution is given by the Mie model, which is described in detail in the Knowledgebase article entitled “How to simulate atmospheric scattering using a Mie model”.
The Phosphor DLL requires 9 inputs:
1. Mean Path: This input is provided at the top of the dialog box, above the specification for the DLL file name. The value corresponds to the mean-free path (in lens units) for fluorescence to occur in the volume.
2-5. Particle Index, Size (microns), Density (cm-3), Min. thresh.: These inputs are required to specify the Mie scattering distribution. Full details on each input are provided in the Knowledgebase article entitled “How to simulate atmospheric scattering using a Mie model”. Note that the Mie distribution is calculated for each wavelength (actually for each unique value of the normalized scattering particle size, where the wavelength is used for normalization), and thus the mean-free path for bulk scattering will vary with wavelength.
6-7. Blue Min, Blue Max (microns): These inputs define the range of wavelengths defined as “blue” light, i.e. light that can undergo both fluorescence and bulk scattering. Any light outside of this wavelength range may undergo bulk scattering but not fluorescence.
In order for this DLL to work correctly, all wavelengths in the system must be defined in the Wavelength Data dialog box, i.e. all sources must use “System Wavelengths” for their Source Color definition. In addition, at least one fluorescent transition must be defined in the “Wavelength Shift” dialog box on the right side of the Volume Physics tab(see the Knowledgebase article entitled “How to model fluorescence via bulk scattering” for more details).
8-9. Fluorescent trans., Scattering trans.: These inputs define attenuation factors for any rays that undergo fluorescence or scattering, respectively. These factors allow the user the account for absorption of energy during either the fluorescence or bulk scattering event (the latter meant to indicate absorption in the scattering sphere).
The “Angle” parameter is not used by the DLL.. Similarly the DLL will be ignored if the input value for the particle index or particle size is <= 0.0, if the input for the particle density is < 0.0, if the minimum or maximum wavelengths for “blue” light are <= 0.0, or if the maximum wavelength for “blue” light is less than the minimum wavelength.
If the particle density is set exactly to 0.0, then fluorescence may still occur inside of the volume but not bulk scattering. While this case serves as a good test of the DLL, it would be more computationally efficient to use the Angle Scattering model instead if you wish to exclude Mie scattering from the volume.
The input values for the Mie parameters are used to calculate the mean-free path for Mie scattering as a function of wavelength. Based on this value and the input value for the fluorescence mean-free path, the DLL uses a Monte Carlo algorithm to determine whether a given ray undergoes scattering, fluorescence (if possible, i.e. if it is a “blue” ray), or simply passes through the volume. The trajectory of the ray is then modified according to the result.
An archive (ZAR) file is provided as an article attachment. In that file, a simple model of a phosphorescent LED has been constructed.
The input blue source is modeled using a Source File from Osram. The wavelength of the source is defined by Wavenumber = 1:
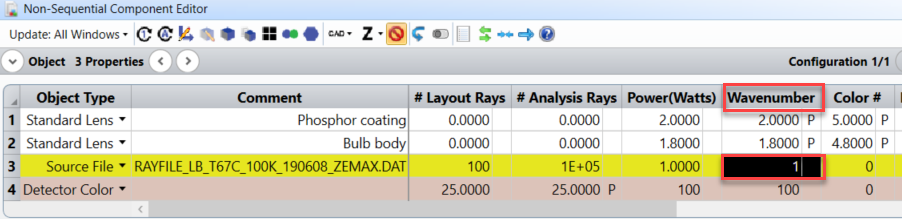
corresponding to a wavelength of 0.46 microns:
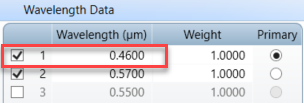
This source is placed inside of a bulb modeled using the Standard Lens object. For this simple example no material has been assigned to the bulb, nor have any scattering properties been assigned to bulb; material and scattering properties should of course be added to a real design accurately reflect the experimental setup.
The phosphor coating in which both fluorescence and scattering occur is modeled as a thin layer outside of the main bulb. This thin layer is actually modeled using another Standard Lens object, taking advantage of the nesting rules in OpticStudio which indicate that when two (or more) volumes overlap in space the properties of the volume listed later in the Non-Sequential Component Editor take precedence. Thus, the bulb is listed after the scattering volume in the editor. The properties of the scattering volume are listed under the Volume Physics tab:
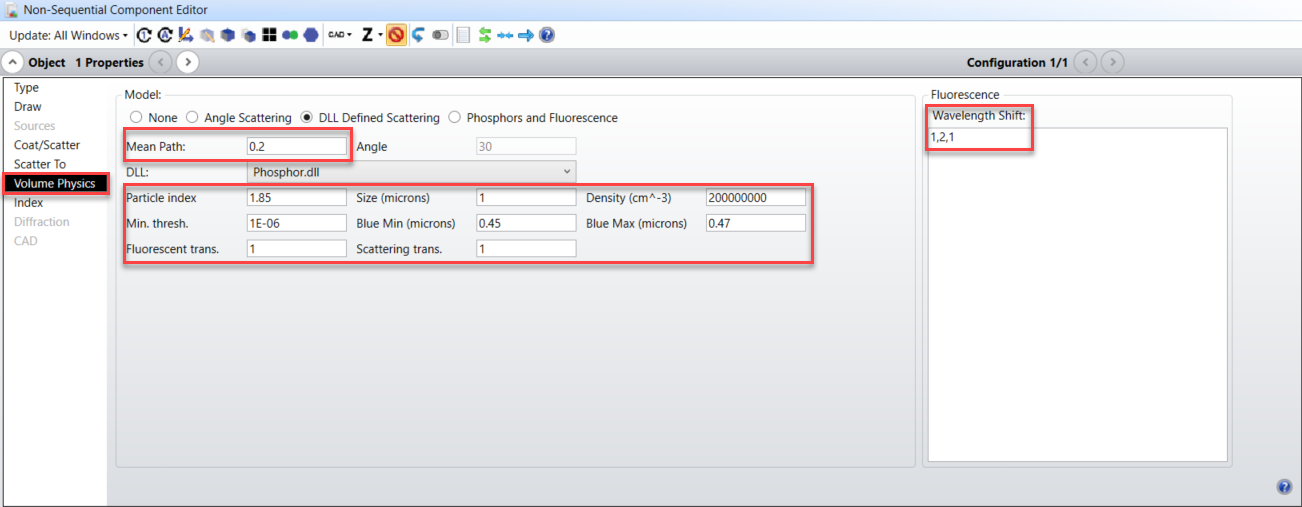
The mean-free path for fluorescence has been set to 0.2 mm, while the wavelength-dependent mean-free path for Mie scattering is determined from the particle index (1.85), size (1 micron), and density (2 x 108 particles/cm3). Any light between 0.45 and 0.47 microns may undergo both scattering and fluorescence, and we assume that no energy is lost during either fluorescence or scattering (transmission values set to unity). The “Wavelength Shift” input indicates that if “blue” light does undergo fluorescence, there is a 100% probability that this light will change wavelengths from wavenumber 1 to wavenumber 2; in our system, wavenumber 2 corresponds to a wavelength of 0.57 microns (see previous picture).
This last statement may seem unnecessary – after all, by definition, the wavelength of light changes during fluorescence. But recall that in OpticStudio fluorescence itself is modeled as a bulk scattering event. Thus, in OpticStudio we can model a volume in which light bulk scatters according to a particular distribution (e.g. Mie) without undergoing fluorescence, but in this same volume any light which does undergo fluorescence may be re-emitted within the same (Mie) distribution. In such a case, we need to explicitly provide the fractional probabilities for light to change wavelength. For the phosphor model, the “scatter” distributions for fluorescence and bulk scattering are unique and explicitly defined, as thus the fractional probability for light to change wavelength is always unity.
Note that the default operation of the "Wavelength Shift" input is to implement a change in wavelength during scattering according to the defined probabilities. The dialog does itself not distinguish between fluorescence scattering and Mie scattering. To provide this distinction, a flag is provided via the value returned in the data[10] entry in the DLL. If the data[10] value is negative, then OpticStudio will ignore wavelength shifting during scattering (set data[10] = -2 for full polarization data to be returned, or to -1 otherwise). For positive values of the data[10] entry, wavelength shifting will occur according to the defined probabilities (set data[10] = 2 for full polarization data to be returned, or to 1 otherwise). The sign of the data[10] value returned by the DLL allows "blue" light rays to undergo both fluorescence scattering (data[10] > 0) and Mie scattering (data[10] < 0).
Any light at wavenumber = 2, corresponding to a wavelength of 0.57 microns, can also undergo Mie scattering in the scattering volume. The calculations in the DLL provide the correct mean-free path for Mie scattering at this wavelength as well as for the input beam wavelength (0.46 microns).
Since the source is inside of a bulb which itself is inside of another volume, the “Inside Of” flag needs to be set for both the source and the bulb. The resultant emission is then measured on a Detector Color object. The results indicate a central emission that is white:

These results may be quantified using the NSDE operand in the Merit Function Editor. The results indicate that the average chromaticity values on the detector are x = 0.33 and y = 0.35. More information on the meaning of these values and the use of the NSDE operand may be found in the Knowledgebase article entitled “How to measure and optimize color data”.
References
KA-01708

Comments
Article is closed for comments.