The Contrast Loss Map in OpticStudio provides an easy way to understand how contrast varies or is lost in an optical system. It visualizes contrast loss for a specific frequency of the Modulation Transfer Function (MTF) as a distribution map across the exit pupil. The Contrast Loss Map gives insight into how the MTF is degrading across the pupil. You can then use the data to determine what changes to make to your system to improve MTF.
Authored By Michael Cheng
Introduction
The Contrast Loss Map plots the same contrast loss values that are calculated during Contrast Optimization, a capability in OpticStudio that uses the Moore-Elliott method to optimize for MTF at least 30 times faster than traditional methods.
MTF as autocorrelation of the pupil function
The theory of how the MTF can be calculated using the autocorrelation of the pupil function helps explain contrast loss. The theory is described here without derivation.
For a specified field and wavelength in an optical system, you can determine a complex pupil function P(x,y) by tracing rays from the object to the image, and then tracing those rays back to the exit pupil. This complex pupil function can be described by:
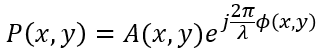
where A(x,y) is the amplitude, λ is the wavelength, and ϕ(x, y) is the optical path difference of the ray that is referenced to the chief ray on the exit pupil. The phase part ϕ(x, y) is known as the wavefront. To see the wavefront in OpticStudio, navigate to Analyze...Wavefront...Wavefront Map.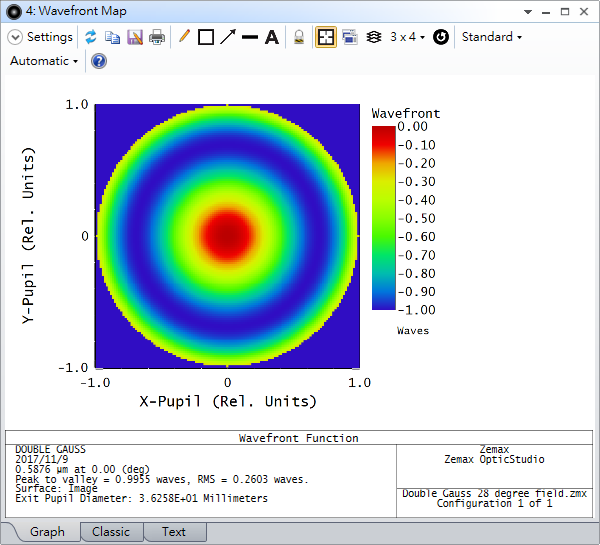
For a specific field and wavelength, the MTF can be calculated by using the modulus of the autocorrelation of P(x,y), which is normalized by the point ξx=ξy=0, where ξx and ξy are the spatial frequency in the x- and y-direction, respectively. That is, the MTF can be described as a function of spatial frequency by:
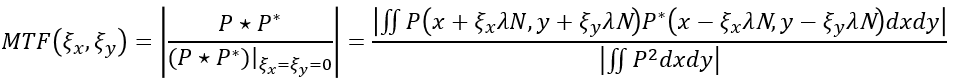
where P* is the complex conjugate of P, λ is the wavelength, and N is the working f-number, which can also be written as F/#. For more information about the definition of the working f-number in OpticStudio, see “Working F/#” in the OpticStudio Help Files. Because the MTF is a two-dimensional distribution over the frequency domain, you can calculate the MTF at a specific frequency, ξt, in x- or y-direction by first shifting the pupil function by 2ξtλN, calculating the complex conjugate, multiplying it by the unshifted pupil function, integrating over the overlap area between the shifted and unshifted pupil function, and then calculating its modulus. For simplicity, you can write the shift amount 2ξtλN as:
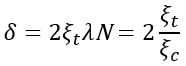
where ξc is the cutoff frequency, and
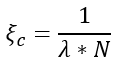 .
.
The following figure shows how pupil function P is shifted by δ in x-direction.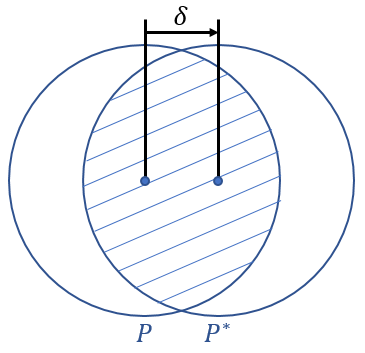
Given the form of δ, notice that δ = 2 when ξt = ξc. This condition corresponds to a pupil shift equal to the normalized pupil diameter. That is, the edges P and P* are coincident, but P and P* do not overlap, resulting in an MTF equal to zero. For more information about normalized pupil diameter, see “Normalized Pupil Coordinates” in the OpticStudio Help Files.
The autocorrelation method is also used to calculate the MTF value when defining the parameter ‘Grid = 0’ for merit function operands MTFT, MTFS, and MTFA. For more information about MTF, see the articles, "How to Optimize on MTF" and "What Does the Sampling Correspond to in Wavefront-Based Calculations?" in the Knowledgebase.
Phase difference and contrast loss
Given that the MTF is calculated as an autocorrelation of the pupil function, multiplication of the two overlapped points from the unshifted pupil P and the shifted pupil P* is equivalent to multiplication of two points that are separated by δ on the unshifted P.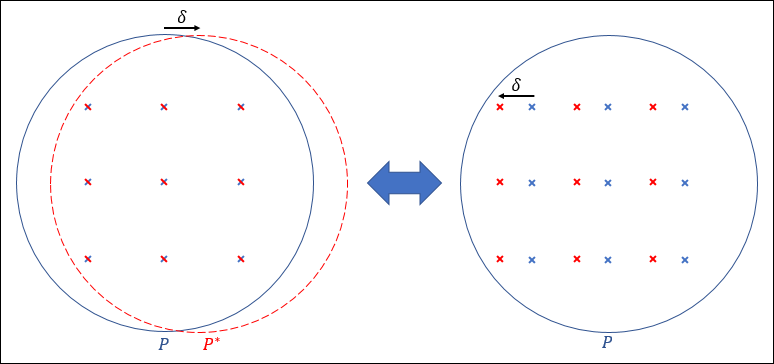
If we numerically consider the MTF equation in previous section, we can write the integration as a summation of sampling points as below.
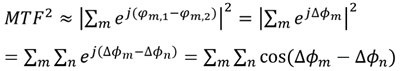
where the Δφm is the phase difference (φm,1 – φm,2) between shifted and unshifted pupil function on the sampling point m.
Therefore, to maximize the MTF for a specific frequency, the phase difference (ϕ1 - ϕ2) of any two rays that are from the same field and separated by δ on the pupil function should be zero or an integer multiple of 2π. For this reason, when optimizing a system using Contrast Optimization, OpticStudio attempts to minimize the phase difference between the pairs of sampled rays. For more information about Contrast Optimization, see the Knowledgebase article, "Optimizing for MTF Performance using Contrast Optimization". Although phase differences are minimized when optimizing for MTF, it is the cosine of the phase difference that contributes to the contrast. The Moore-Elliott method uses the cosine of the phase difference to calculate the contrast loss of each sampling point in the pupil, as described by: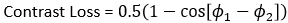
where ϕ1 and ϕ2 are the phase of the two rays from the same field. When calculating sagittal contrast loss, the two rays are separated by δ in Px direction. When calculating tangential contrast loss, the two rays are separated by δ in Py direction. For a more information about the Moore-Elliot method, see Reference 1 at the end of this article.
Visualization of contrast loss
The Contrast Loss Map displays the phase difference and contrast loss on a plot, which can be used to analyze and improve an optical system. As shown in the following image, the Contrast Loss Map displays the contrast loss and wavefront information for each sampling point in the pupil. Each sample point is represented by a circle and small indicator line, respectively. To find this analysis in OpticStudio, navigate to Analyze...Wavefront...Contrast Loss Map or Analyze...MTF...Contrast Loss Map.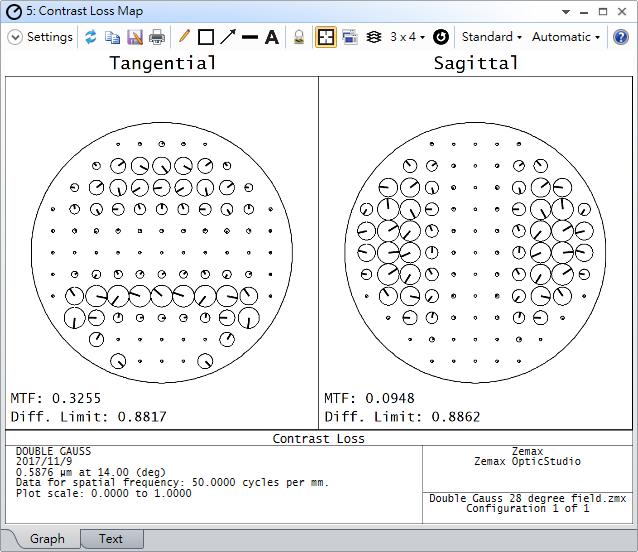
The size of each circle represents the magnitude of the contrast loss at that position in the pupil. The circle’s magnitude is at a maximum when contrast loss is 1 and at a minimum when contrast loss is 0. The orientation of the indicator line represents the wavefront information. For each point on the pupil, the average optical path difference (OPD) of the shifted and unshifted pupil function is calculated, and the modulo 2π is taken. This value determines the orientation of the indicator, as shown in the following image. When the OPD is zero, the indicator points to the +X direction and rotates counterclockwise as the average OPD increases.
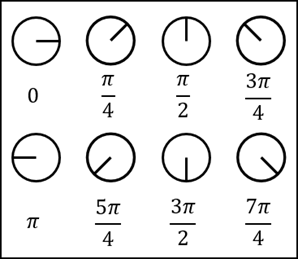
For more information about how OpticStudio calculates contrast loss, see “Contrast Loss Map” in the OpticStudio Help Files.
The Contrast Loss Map indicates for a specific field and wavelength which portions of the beam, in pupil coordinates, have a contrast lower than 1, and thus an MTF less than the diffraction limited MTF. Consider a doublet with a field of view of 5 degrees, as shown in the following image. The radii of curvature for this doublet are optimized using Contrast Optimization for a spatial frequency of 20 cycles/mm.
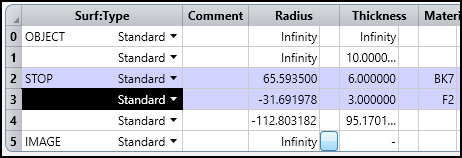
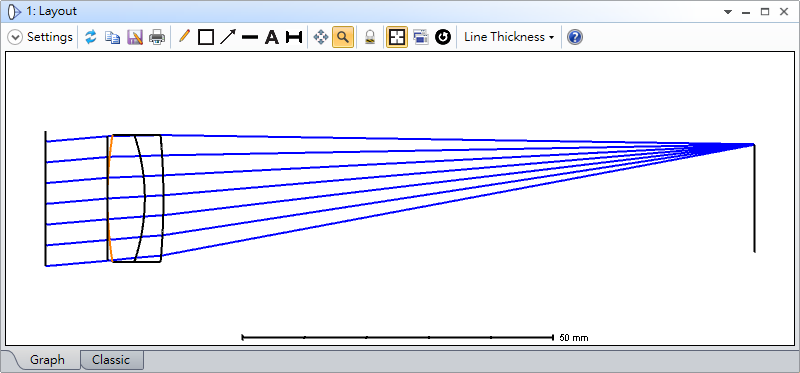
The images below show the MTF and Contrast Loss Map (20 cycles/mm).
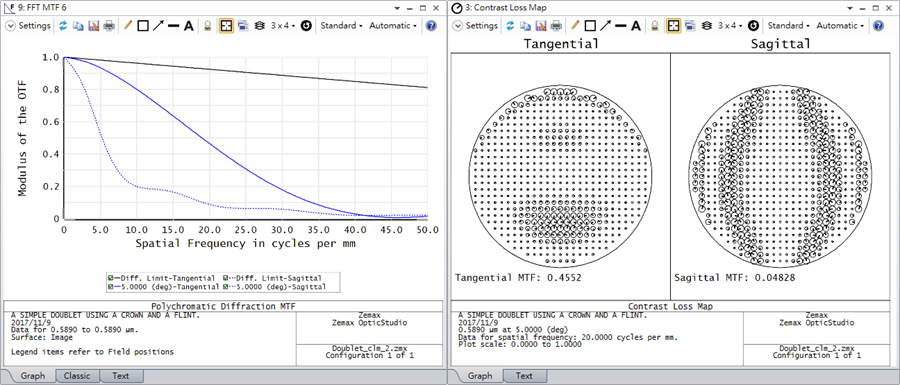
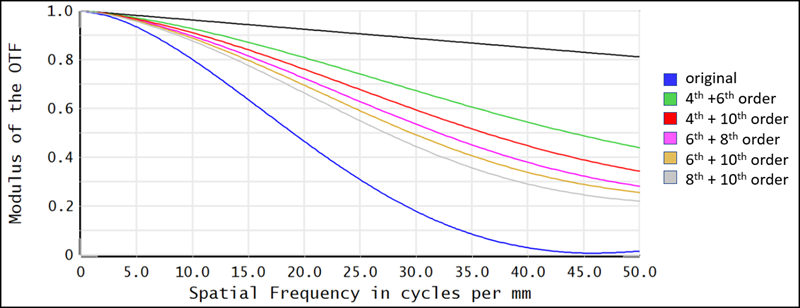
To increase the tangential MTF, we can change the first surface of the doublet to an Even Asphere surface, and then optimize this new system by adding a single aspheric coefficient as a variable. The following plot displays the resulting MTF when using each coefficient order during optimization. The black curve displays the diffraction limited MTF.
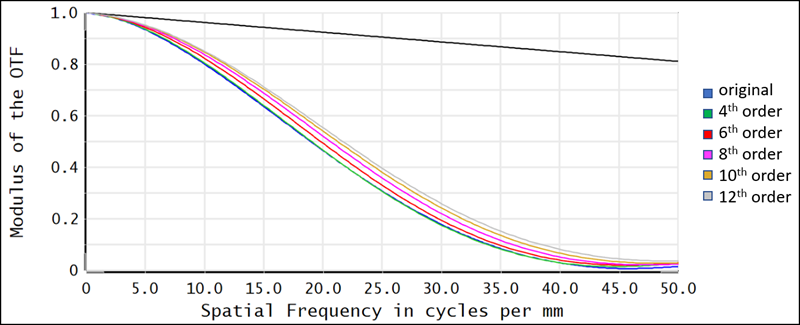
The results indicate that the MTF is only slightly improved in each case. To understand why this is, you can analyze the sag of each resulting surface. In this case, optimizing using a single coefficient only significantly changes the surface sag near the edges of the lens. As shown in the following image, the 12th order aspheric coefficient contributes most to the sag at the edge of the aspheric surface. The 12th order coefficient also leads to the highest MTF.
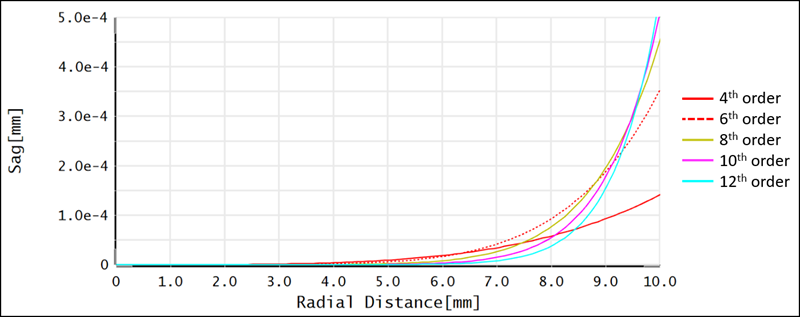
As shown in the following image, when comparing the Contrast Loss Map before and after optimizing the 12th order aspheric coefficient, it is clear that the contrast loss at the edge of the pupil is eliminated, which contributes to a small increase of MTF. However, the changes to the surface edges do not significantly impact the tangential Contrast Loss Map.
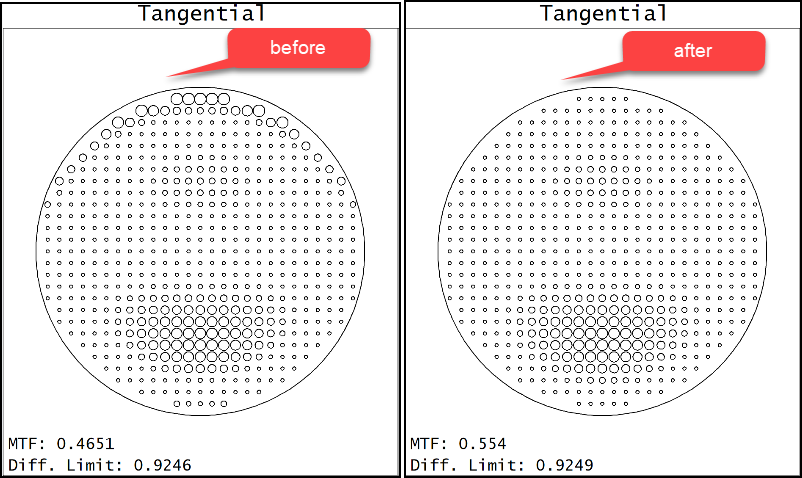 Therefore, you can assume that to eliminate the “bump” in the tangential contrast loss map, you need to optimize at least two aspheric coefficients, because one coefficient alone does not sufficiently control the surface shape in the area between the center and edge of the aperture. As shown in the following image, the MTF improves much more significantly for a variety of coefficient combinations when coefficients are optimized at the same time.
Therefore, you can assume that to eliminate the “bump” in the tangential contrast loss map, you need to optimize at least two aspheric coefficients, because one coefficient alone does not sufficiently control the surface shape in the area between the center and edge of the aperture. As shown in the following image, the MTF improves much more significantly for a variety of coefficient combinations when coefficients are optimized at the same time.
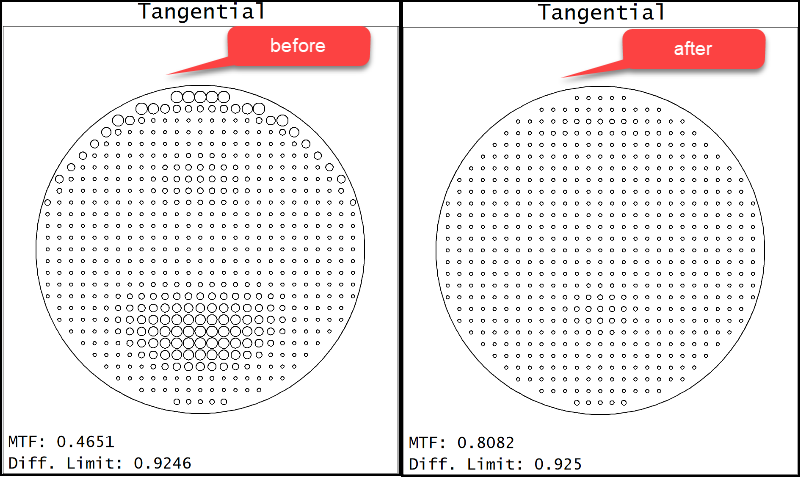
Additionally, when analyzing the Contrast Loss Map and sag contribution of the optimization result using the 4th and 6th order coefficients, you see that the “bump” is greatly reduced.
 When checking the sag contribution from the 4th and 6th order aspheric coefficients, you notice that the sag changes are mainly in the area between the center and edge of the aperture. These have a similar position to the “bump” in tangential contrast loss map before optimization, as shown in the following image.
When checking the sag contribution from the 4th and 6th order aspheric coefficients, you notice that the sag changes are mainly in the area between the center and edge of the aperture. These have a similar position to the “bump” in tangential contrast loss map before optimization, as shown in the following image.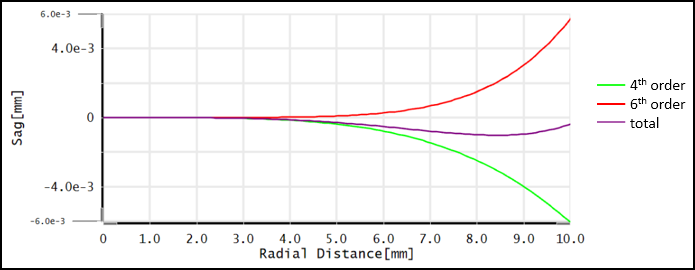 This example demonstrates how using the Contrast Loss Map feature in OpticStudio can reveal what surface shape or change to the surface shape can help optimize the MTF at a specific spatial frequency.
This example demonstrates how using the Contrast Loss Map feature in OpticStudio can reveal what surface shape or change to the surface shape can help optimize the MTF at a specific spatial frequency.
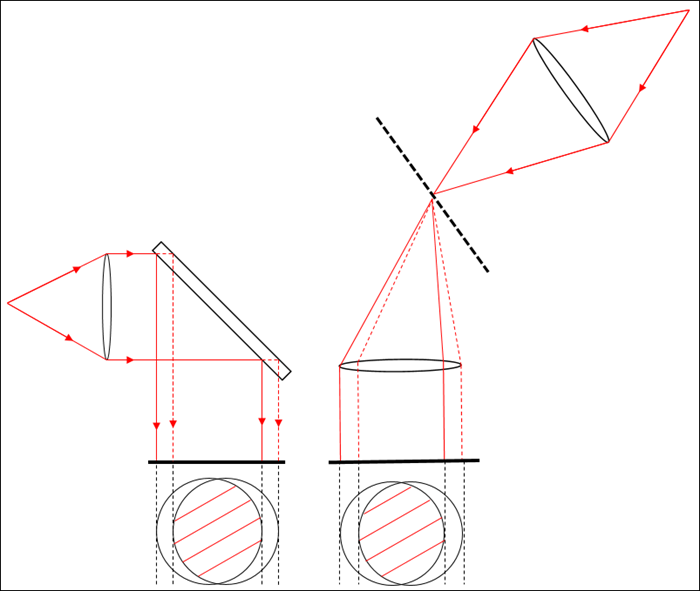
Shearing interferogram
Because contrast loss is based on the cosine of the phase difference, when it is used with high sampling, the Contrast Loss Map can simulate a shearing interferogram. Shearing interferometers split a test beam in two and propagate the resulting beams in the same direction, but with slightly offset lateral positions. The following image shows two example schematics. The schematic on the left demonstrates splitting the test beam using a flat glass plate; the schematic on the right demonstrates splitting the test beam using a diffraction grating. The shearing interferogram is the interference pattern of the two beams on the detector. For more information about shearing interferometers, refer to the Wikipedia article, “Shearing interferometer.”
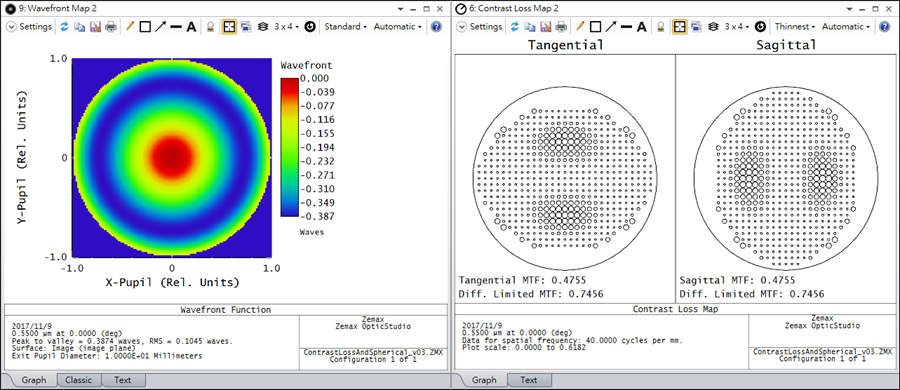
Because the Contrast Loss Map uses an offset pupil in its calculations, it is possible to link its results to real shearing interferogram measurements. For example, in the following system, the Wavefront Map displays obvious spherical aberration. The Contrast Loss Map for the same system shows a typical shearing interferogram pattern that contains spherical aberration.
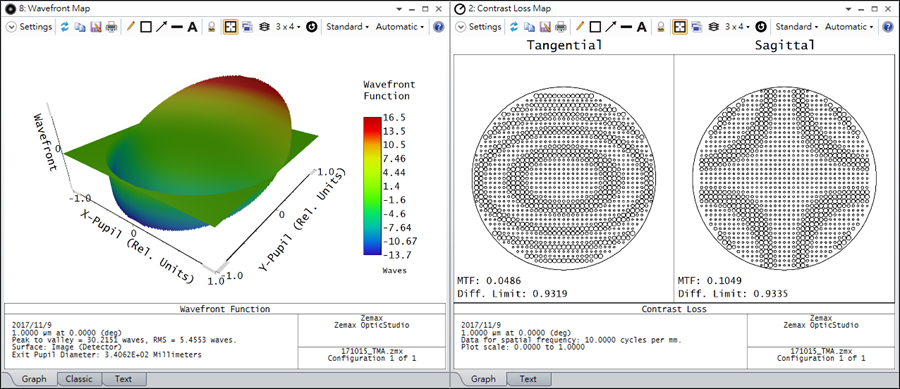
The same is true for the following Wavefront Map which displays coma. The Contrast Loss Map appears just as a shearing interferogram that contains coma would appear.
References
- K. E. Moore, E. Elliott, et. al. "Digital Contrast Optimization - A faster and better method for optimizing system MTF," in Optical Design and Fabrication 2017 (Freeform, IODC, OFT), OSA Technical Digest (online) (Optical Society of America, 2017), paper IW1A.3.
- Optimizing for MTF Performance using Contrast Optimization
KA-01646

Comments
Article is closed for comments.