Alvarez Zoom is an amazing optical system where optical zoom is provided by lateral shift of free-form lenses. This article explains main principles of Alvarez Zoom lens and includes a demonstration of an Alvarez Zoom lens calculation and modeling in Zemax Optic Studio. A sample file is included.

Authored By Ted Churlyaev, Vadim Vlakhko, Li Han Chan (DynaOptics LCC)

Downloads

Article Attachments

What is Alvarez Zoom lens

One probably knows how traditional zoom lens works. We have several groups of lens elements in an optical system, which move along the optical axis along predefined trajectories providing variation of resulting focal length (zoom factor) of the optical system.

In case of Alvarez Zoom Lens we have pairs of so called Alvarez lenses and the lateral shift of these lens elements with respect to each other provides variation of focal length of the optical system.

Main difference between conventional zoom lens and Alvarez zoom lens is that conventional system lenses are moving along optical axis while Alvarez system lenses are moving in a perpendicular direction to optical axis. Because of this feature Alvarez zoom can be really useful in slim applications like smart phones.

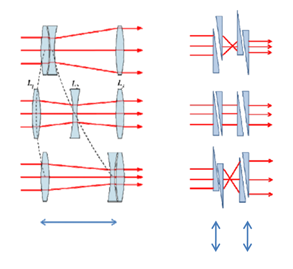
Fig. 1 Conventional Optical Zoom lens (left) and Alvarez Zoom lens (right)

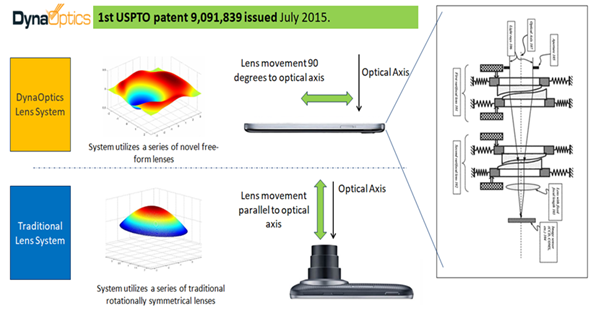
Fig 2. General representation of Alvarez Zoom and its comparison with Conventional Optical Zoom

How Alvarez pairs work

To understand how Alvarez zoom works at first let’s look at Alvarez pairs. Each Alvarez lens is a free-form optical element with only one plain of symmetry. 

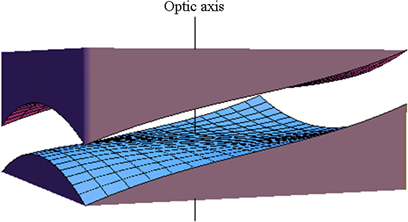
Fig 3. Alvarez pair (picture from www.spiedigitallibrary.org)

As one can see in the picture below, each Alvarez pair represents an optical element with optical power variation. Lateral shift of Alvarez lenses in each pair changes optical power of the Alvarez pair.

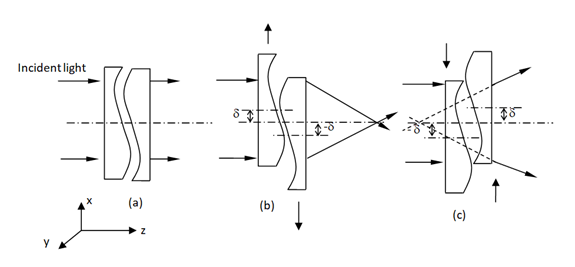
Fig 4. General working principle of an Alvarez lens pair

Paraxial model of an Alvarez Zoom lens

The core of our Alvarez zoom lens is an afocal Galilean system. The first Alvarez pair represents objective lens of Galilean system, while second Alvarez pair represents an eyepiece lens.

Magnification of the Galilean system is

M = -f1/f2                                                                  

Where f1 is focal length of objective lens and f2 is focal length of eyepiece. In an Alvarez zoom lens the objective lens and eyepiece are represented by Alvarez pairs which means we can change focal lengths f1 and f2, so we can continuously change magnification of the system, thus we can do zooming.

Galilean system is an afocal system therefore to focus image on the sensor plane we introduce a Base Lens – an optical component with fixed focus.

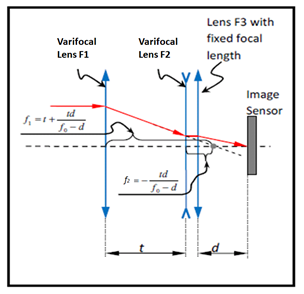
Fig 5. Paraxial layout of Alvarez Zoom lens

Focal lengths of components can be calculated from the following equations:

 

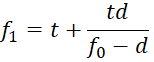
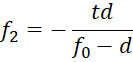
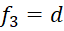
Let’s assign some numbers as an example and calculate our first paraxial model.

FOV (field of view): Requirement from a customer, for example 70 degree at wide angle.

HFOV: half of the FOV.

Sensor size: the selected sensor, for example 1/3.06” sensor (Diagonal image height = 2.933mm).

Zoom ratio: Effective focal length at telephoto end (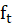)/Effective focal length at wide angle end (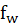).Let’s suppose we want to have a 3x zoom lens.

Effective focal length at wide angle end:

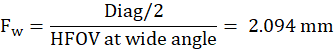
Effective focal length at telephoto end:

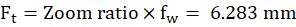
HFOV at telephoto end:

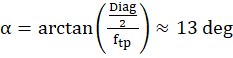
so FOV at telephoto end is about 26 degrees

As a start we decided to assign t=20 mm and d = 5 mm. Let’s calculate focal lengths of components at wide angle and telephoto positions:

 

 

                                     

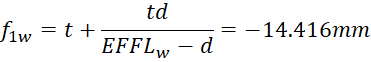
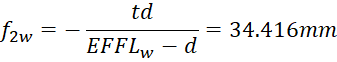
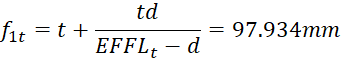
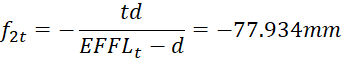
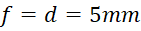
Now we have all the necessary parameters of our paraxial model.

Modeling Alvarez Zoom lens in Zemax Optic Studio

Let’s convert first and second paraxial groups to real Alvarez lenses. As a first approach it is convenient to use Extended Polynomial. Using following equations we can calculate sag of Alvarez pairs:

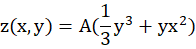
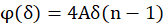
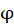 is optical power of Alvarez pair corresponding to lateral shift of lenses in the Alvarez pair

A is extended polynomial‘s coefficient

δ is lateral shift of lenses in Alvarez pair, it should be a nonzero value since we know that with zero shift the Alvarez pair would be simply a parallel-sided plate with optical power being zero.

Let’s assign for wide angle position lateral shift of lenses in each Alvarez pair to be 1 mm, e.g. δ_1w = 1 mm and δ_2w = 1 mm.

As a material we choose optical plastic APL5014CL from APEL catalog available in Zemax Optic Studio, refractive index n = 1.5445.

Having this data, we can calculate extended polynomial ‘s coefficient A.

For the first Alvarez pair:

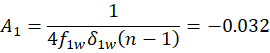
For the second Alvarez pair:

 

 

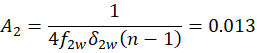
Lateral shift of lenses in each Alvarez pair at telephoto position can be calculated as:

  

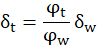
Taken that 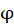 is inversion of focal length we will get following values:

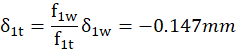
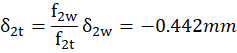
It seems now we have all the data to model our Alvarez Zoom lens in ZemaxOpticStudio.

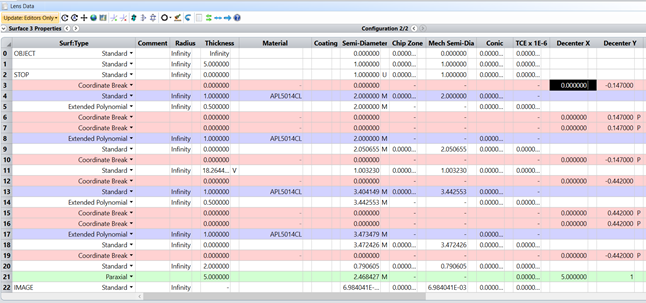
Fig 6. Modeling Alvarez Zoom lens in OpticStudio: Lens Data Editor (left side)

To model lateral shift of Alvarez lenses we use Coordinate Breaks. Every second Coordinate Break returns coordinate system back to original.

For simplicity of this calculation Base Lens currently is represented as just a paraxial lens.

All Extended Polynomial surfaces have 9 terms and Norm Radius equals 1. For the first Alvarez pair we set up X2Y1 term to be equal early calculated A1, and X0Y3 term to be equal A1/3. And correspondingly for the second Alvarez pair X2Y1 term to be equal A2, and X0Y3 term to be equal A2/3.

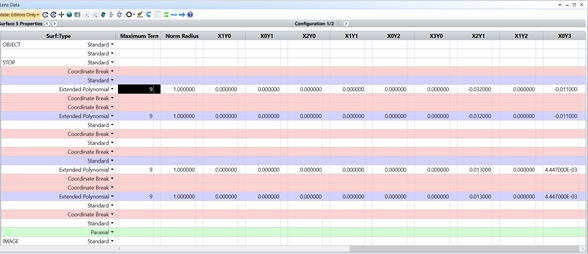
Fig 7. Modeling Alvarez Zoom lens in OpticStudio: Lens Data Editor (right side)

Now let’s go to the Multi-Configuration Editor and set up corresponding lateral shifts of Alvarez lenses.

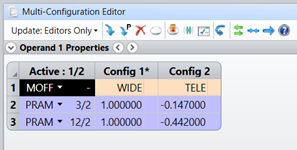
Fig 8. Modeling Alvarez Zoom lens in OpticStudio: Multi-Configuration Editor

In the picture below one can see wide angle and telephoto configurations together.

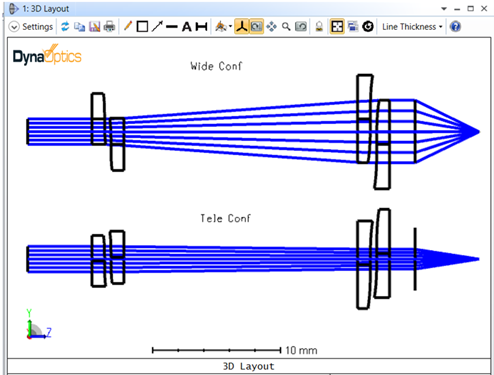
Fig 9. Modeling Alvarez Zoom lens in OpticStudio: 3D Layout

One can probably notice that in the Lens Data Editor the distance between the first and the second Alvarez pairs is not exactly 20 mm as we assigned in our calculations. The idea is that we did calculations for thin components but now our Alvarez lenses have some nonzero thickness, so we simply set the distance between them to be variable in the Lens Data Editor, insert simple Default Merit Function and run optimization with only one variable. After that our 20 mm turned into 18.2644 mm.

Since we are using decentered Extended Polynomial surfaces paraxial value EFFL calculated in Zemax OpticStudio will be incorrect. To calculate focal length of the system we can use a real ray which is close enough to the optical axis (see the picture below).

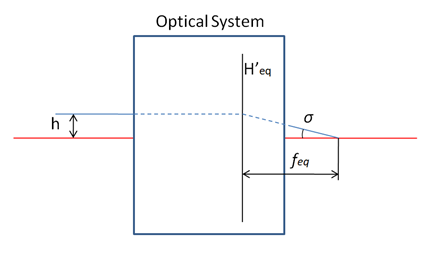
Fig 10. Focal length calculation method for Alvarez Zoom lens

Knowing σ and h it is easy to calculate effective focal length of the optical system. We simply did this calculation in the Merit Function Editor and got 2.135 mm focal length for wide angle configuration and 6.306 mm focal length for telephoto configuration. As one can see these values are very close to the target values, which means the optical system works correctly.

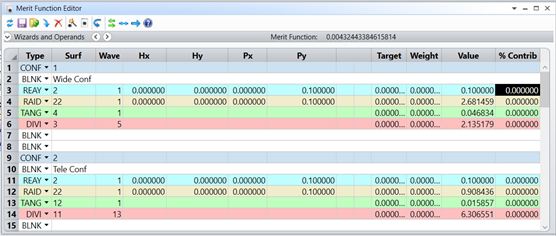
Fig 11. Modeling Alvarez Zoom lens in OpticStudio: Merit Function Editor

Since it is a paraxial model it would be somehow accurate only for small angles, to correct aberrations along whole field of view we should add more terms to extended polynomial surfaces and optimize the optical system.

In the described Zemax model we set diameter of the entrance pupil equal 2 mm. Actually, this value was chosen for illustrational purposes only, since with this value shape of Alvarez pairs looks clearer on the plots. But it is easy to calculate that such entrance pupil diameter providesF/# ≈1 for wide angle configuration which is pretty extreme, and it would be hard to correct aberrations for such a large aperture. We would recommend to proceed optimization with a smaller aperture first. But of course, at the end of the optimization one should get to the value which satisfies costumer’s F/# request.

Another thing is that aperture stop in this model is placed in front of the optical system. But at some moment one may find it reasonable to place the aperture stop inside the optical system. In this case don’t forget to turn Ray Aiming on.

Real prototype

Although Alvarez lenses were invented in 1967 this engineering idea was significantly ahead of manufacturing capabilities of that time. Manufacturing of such complex free-form optical elements looked hardly possible without modern manufacturing technologies. In the left-hand picture below, one can see an Alvarez lens manufactured using plastic molding technology.In the right-hand picture one can see DynaOptics’ prototype of Alvarez Zoom lens.

If you have further interest or questions about Alvarez Zoom lens or free-form optics please feel free to contact Ted (ted@dynaoptics.com) or Vadim (vadim@dynaoptics.com) at DynaOptics.

 

 

 

 

 

 

 

Fig 12. Plastic Alvarez lens (left) Alvarez Zoom lens prototype (right)

References

1. Patent US10082652B2“Miniaturized optical zoom lens system”
   https://patents.google.com/patent/US10082652B2
    
2. Paul J. Smilie, Thomas J. Suleski, Brian Dutterer, Jennifer L. Lineberger, Matthew A. Davies,“Design and characterization of an infrared Alvarez lens”.
   https://www.spiedigitallibrary.org/ContentImages/Journals/OPEGAR/51/1/013006/FigureImages/OE_51_1_013006_f001.png
    
3. https://www.dynaoptics.com/

KA-01985